145 lines
3.6 KiB
Markdown
145 lines
3.6 KiB
Markdown
|
|
## 题目地址(1260. 二维网格迁移)
|
|||
|
|
|
|||
|
|
https://leetcode-cn.com/problems/shift-2d-grid/description/
|
|||
|
|
|
|||
|
|
## 题目描述
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
给你一个 n 行 m 列的二维网格 grid 和一个整数 k。你需要将 grid 迁移 k 次。
|
|||
|
|
|
|||
|
|
每次「迁移」操作将会引发下述活动:
|
|||
|
|
|
|||
|
|
位于 grid[i][j] 的元素将会移动到 grid[i][j + 1]。
|
|||
|
|
位于 grid[i][m - 1] 的元素将会移动到 grid[i + 1][0]。
|
|||
|
|
位于 grid[n - 1][m - 1] 的元素将会移动到 grid[0][0]。
|
|||
|
|
请你返回 k 次迁移操作后最终得到的 二维网格。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
示例 1:
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
输入:grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
|
|||
|
|
输出:[[9,1,2],[3,4,5],[6,7,8]]
|
|||
|
|
示例 2:
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
输入:grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
|
|||
|
|
输出:[[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]
|
|||
|
|
示例 3:
|
|||
|
|
|
|||
|
|
输入:grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
|
|||
|
|
输出:[[1,2,3],[4,5,6],[7,8,9]]
|
|||
|
|
|
|||
|
|
|
|||
|
|
提示:
|
|||
|
|
|
|||
|
|
1 <= grid.length <= 50
|
|||
|
|
1 <= grid[i].length <= 50
|
|||
|
|
-1000 <= grid[i][j] <= 1000
|
|||
|
|
0 <= k <= 100
|
|||
|
|
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
## 暴力法
|
|||
|
|
|
|||
|
|
我们直接翻译题目,没有任何 hack 的做法。
|
|||
|
|
|
|||
|
|
### 代码
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
from copy import deepcopy
|
|||
|
|
|
|||
|
|
class Solution:
|
|||
|
|
def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:
|
|||
|
|
n = len(grid)
|
|||
|
|
m = len(grid[0])
|
|||
|
|
for _ in range(k):
|
|||
|
|
old = deepcopy(grid)
|
|||
|
|
for i in range(n):
|
|||
|
|
for j in range(m):
|
|||
|
|
if j == m - 1:
|
|||
|
|
grid[(i + 1) % n][0] = old[i][j]
|
|||
|
|
elif i == n - 1 and j == m - 1:
|
|||
|
|
grid[0][0] = old[i][j]
|
|||
|
|
else:
|
|||
|
|
grid[i][j + 1] = old[i][j]
|
|||
|
|
return grid
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
由于是 easy,上述做法勉强可以过,我们考虑优化。
|
|||
|
|
|
|||
|
|
## 数学分析
|
|||
|
|
|
|||
|
|
### 思路
|
|||
|
|
|
|||
|
|
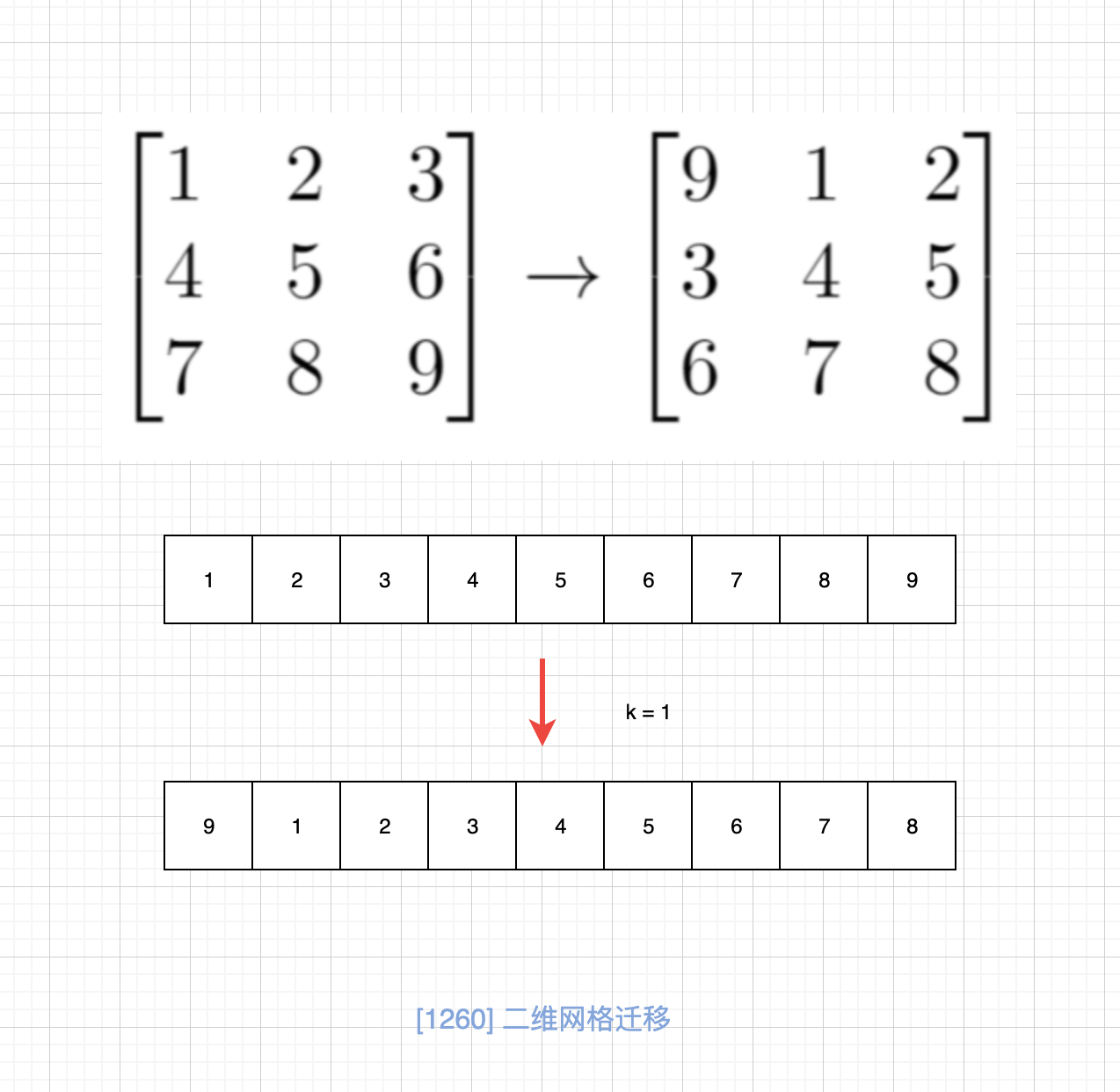
我们仔细观察矩阵会发现,其实这样的矩阵迁移是有规律的。 如图:
|
|||
|
|
|
|||
|
|
|
|||
|
|
因此这个问题就转化为我们一直的一维矩阵转移问题,LeetCode 也有原题[189. 旋转数组](https://leetcode-cn.com/problems/rotate-array/),同时我也写了一篇文章[文科生都能看懂的循环移位算法](https://lucifer.ren/blog/2019/12/11/rotate-list/)专门讨论这个,最终我们使用的是三次旋转法,相关数学证明也有写,很详细,这里不再赘述。
|
|||
|
|
|
|||
|
|
LeetCode 真的是喜欢换汤不换药呀 😂
|
|||
|
|
|
|||
|
|
### 代码
|
|||
|
|
|
|||
|
|
Python 代码:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
#
|
|||
|
|
# @lc app=leetcode.cn id=1260 lang=python3
|
|||
|
|
#
|
|||
|
|
# [1260] 二维网格迁移
|
|||
|
|
#
|
|||
|
|
|
|||
|
|
# @lc code=start
|
|||
|
|
|
|||
|
|
|
|||
|
|
class Solution:
|
|||
|
|
def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:
|
|||
|
|
n = len(grid)
|
|||
|
|
m = len(grid[0])
|
|||
|
|
# 二维到一维
|
|||
|
|
arr = [grid[i][j] for i in range(n) for j in range(m)]
|
|||
|
|
# 取模,缩小k的范围,避免无意义的运算
|
|||
|
|
k %= m * n
|
|||
|
|
res = []
|
|||
|
|
# 首尾交换法
|
|||
|
|
|
|||
|
|
def reverse(l, r):
|
|||
|
|
while l < r:
|
|||
|
|
t = arr[l]
|
|||
|
|
arr[l] = arr[r]
|
|||
|
|
arr[r] = t
|
|||
|
|
l += 1
|
|||
|
|
r -= 1
|
|||
|
|
# 三次旋转
|
|||
|
|
reverse(0, m * n - k - 1)
|
|||
|
|
reverse(m * n - k, m * n - 1)
|
|||
|
|
reverse(0, m * n - 1)
|
|||
|
|
# 一维到二维
|
|||
|
|
row = []
|
|||
|
|
for i in range(m * n):
|
|||
|
|
if i > 0 and i % m == 0:
|
|||
|
|
res.append(row)
|
|||
|
|
row = []
|
|||
|
|
row.append(arr[i])
|
|||
|
|
res.append(row)
|
|||
|
|
|
|||
|
|
return res
|
|||
|
|
|
|||
|
|
# @lc code=end
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
## 相关题目
|
|||
|
|
|
|||
|
|
- [189. 旋转数组](https://leetcode-cn.com/problems/rotate-array/)
|
|||
|
|
|
|||
|
|
## 参考
|
|||
|
|
|
|||
|
|
- [文科生都能看懂的循环移位算法](https://lucifer.ren/blog/2019/12/11/rotate-list/)
|