142 lines
3.9 KiB
Markdown
142 lines
3.9 KiB
Markdown
## 题目地址
|
||
|
||
https://leetcode.com/problems/maximum-product-subarray/description/
|
||
|
||
## 题目描述
|
||
```
|
||
给你一个整数数组 nums ,请你找出数组中乘积最大的连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
|
||
|
||
|
||
|
||
示例 1:
|
||
|
||
输入: [2,3,-2,4]
|
||
输出: 6
|
||
解释: 子数组 [2,3] 有最大乘积 6。
|
||
示例 2:
|
||
|
||
输入: [-2,0,-1]
|
||
输出: 0
|
||
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
|
||
```
|
||
|
||
## 思路
|
||
|
||
这道题目要我们求解连续的 n 个数中乘积最大的积是多少。这里提到了连续,笔者首先想到的就是滑动窗口,但是这里比较特殊,我们不能仅仅维护一个最大值,因此最小值(比如-20)乘以一个比较小的数(比如-10)
|
||
可能就会很大。 因此这种思路并不方便。
|
||
|
||
首先来暴力求解,我们使用两层循环来枚举所有可能项,这种解法的时间复杂度是O(n^2), 代码如下:
|
||
|
||
```js
|
||
var maxProduct = function(nums) {
|
||
let max = nums[0];
|
||
let temp = null;
|
||
for (let i = 0; i < nums.length; i++) {
|
||
temp = nums[i];
|
||
for (let j = i + 1; j < nums.length; j++) {
|
||
temp *= nums[j];
|
||
max = Math.max(temp, max);
|
||
}
|
||
}
|
||
|
||
return max;
|
||
};
|
||
```
|
||
|
||
|
||
|
||
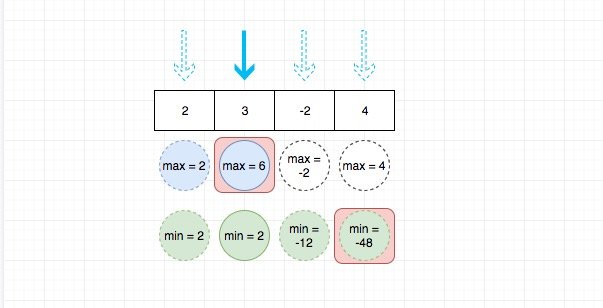
前面说了`最小值(比如-20)乘以一个比较小的数(比如-10)可能就会很大` 。因此我们需要同时记录乘积最大值和乘积最小值,然后比较元素和这两个的乘积,去不断更新最大值。当然,我们也可以选择只取当前元素。因此实际上我们的选择有三种,而如何选择就取决于哪个选择带来的价值最大(乘积最大或者最小)。
|
||
|
||
|
||
|
||
这种思路的解法由于只需要遍历一次,其时间复杂度是O(n),代码见下方代码区。
|
||
|
||
## 关键点
|
||
|
||
- 同时记录乘积最大值和乘积最小值
|
||
## 代码
|
||
|
||
代码支持:Python3,JavaScript
|
||
|
||
|
||
|
||
Python3 Code:
|
||
|
||
|
||
```python
|
||
|
||
|
||
class Solution:
|
||
def maxProduct(self, nums: List[int]) -> int:
|
||
n = len(nums)
|
||
max__dp = [1] * (n + 1)
|
||
min_dp = [1] * (n + 1)
|
||
ans = float('-inf')
|
||
|
||
for i in range(1, n + 1):
|
||
max__dp[i] = max(max__dp[i - 1] * nums[i - 1],
|
||
min_dp[i - 1] * nums[i - 1], nums[i - 1])
|
||
min_dp[i] = min(max__dp[i - 1] * nums[i - 1],
|
||
min_dp[i - 1] * nums[i - 1], nums[i - 1])
|
||
ans = max(ans, max__dp[i])
|
||
return ans
|
||
```
|
||
|
||
|
||
**复杂度分析**
|
||
- 时间复杂度:$O(N)$
|
||
- 空间复杂度:$O(N)$
|
||
|
||
|
||
当我们知道动态转移方程的时候,其实应该发现了。我们的dp[i] 只和 dp[i - 1]有关,这是一个空间优化的信号,告诉我们`可以借助两个额外变量记录即可`。
|
||
|
||
|
||
Python3 Code:
|
||
|
||
|
||
```python
|
||
|
||
class Solution:
|
||
def maxProduct(self, nums: List[int]) -> int:
|
||
n = len(nums)
|
||
a = b = 1
|
||
ans = float('-inf')
|
||
|
||
for i in range(1, n + 1):
|
||
temp = a
|
||
a = max(a * nums[i - 1],
|
||
b * nums[i - 1], nums[i - 1])
|
||
b = min(temp * nums[i - 1],
|
||
b * nums[i - 1], nums[i - 1])
|
||
ans = max(ans, a)
|
||
return ans
|
||
|
||
```
|
||
|
||
JavaScript Code:
|
||
|
||
```js
|
||
var maxProduct = function(nums) {
|
||
let max = nums[0];
|
||
let min = nums[0];
|
||
let res = nums[0];
|
||
|
||
for (let i = 1; i < nums.length; i++) {
|
||
let tmp = min;
|
||
min = Math.min(nums[i], Math.min(max * nums[i], min * nums[i])); // 取最小
|
||
max = Math.max(nums[i], Math.max(max * nums[i], tmp * nums[i])); /// 取最大
|
||
res = Math.max(res, max);
|
||
}
|
||
return res;
|
||
};
|
||
```
|
||
|
||
|
||
**复杂度分析**
|
||
- 时间复杂度:$O(N)$
|
||
- 空间复杂度:$O(1)$
|
||
|
||
更多题解可以访问我的LeetCode题解仓库:https://github.com/azl397985856/leetcode 。 目前已经30K star啦。
|
||
|
||
大家也可以关注我的公众号《脑洞前端》获取更多更新鲜的LeetCode题解
|