6.9 KiB
6.9 KiB
题目地址
https://leetcode.com/problems/min-stack/description/
题目描述
Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.
push(x) -- Push element x onto stack.
pop() -- Removes the element on top of the stack.
top() -- Get the top element.
getMin() -- Retrieve the minimum element in the stack.
Example:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> Returns -3.
minStack.pop();
minStack.top(); --> Returns 0.
minStack.getMin(); --> Returns -2.
差值法
思路
符合直觉的方法是,每次对栈进行修改操作(push和pop)的时候更新最小值。 然后getMin只需要返回我们计算的最小值即可, top也是直接返回栈顶元素即可。 这种做法每次修改栈都需要更新最小值,因此时间复杂度是O(n).
是否有更高效的算法呢?答案是有的。
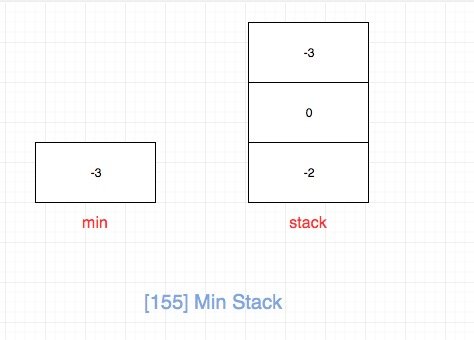
我们每次入栈的时候,保存的不再是真正的数字,而是它与当前最小值的差(当前元素没有入栈的时候的最小值)。 这样我们pop和top的时候拿到栈顶元素再加上上一个最小值即可。 另外我们在push和pop的时候去更新min,这样getMin的时候就简单了,直接返回min。
注意上面加粗的“上一个”,不是“当前的最小值”
经过上面的分析,问题的关键转化为“如何求得上一个最小值”,解决这个的关键点在于利用min。
pop或者top的时候:
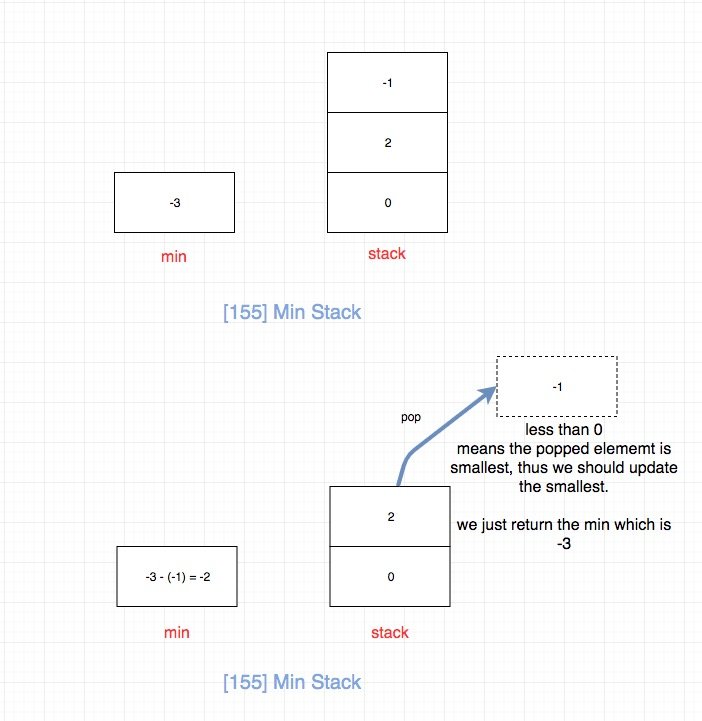
- 如果栈顶元素小于0,说明栈顶是当前最小的元素,它出栈会对min造成影响,我们需要去更新min。 上一个最小的是“min - 栈顶元素”,我们需要将上一个最小值更新为当前的最小值
因为栈顶元素入栈的时候的通过
栈顶元素 = 真实值 - 上一个最小的元素得到的, 而真实值 = min, 因此可以得出上一个最小的元素 = 真实值 -栈顶元素
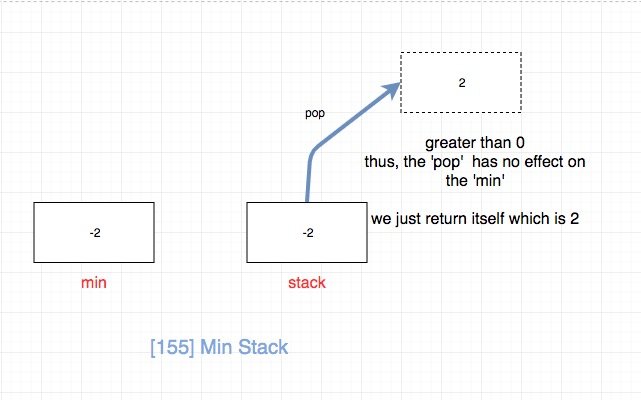
- 如果栈顶元素大于0,说明它对最小值
没有影响,上一个最小值就是上上个最小值。
关键点
- 最小栈存储的不应该是真实值,而是真实值和min的差值
- top的时候涉及到对数据的还原,这里千万注意是上一个最小值
代码
- 语言支持:JS,Python
Javascript Code:
/*
* @lc app=leetcode id=155 lang=javascript
*
* [155] Min Stack
*/
/**
* initialize your data structure here.
*/
var MinStack = function() {
this.stack = [];
this.minV = Number.MAX_VALUE;
};
/**
* @param {number} x
* @return {void}
*/
MinStack.prototype.push = function(x) {
// update 'min'
const minV = this.minV;
if (x < this.minV) {
this.minV = x;
}
return this.stack.push(x - minV);
};
/**
* @return {void}
*/
MinStack.prototype.pop = function() {
const item = this.stack.pop();
const minV = this.minV;
if (item < 0) {
this.minV = minV - item;
return minV;
}
return item + minV;
};
/**
* @return {number}
*/
MinStack.prototype.top = function() {
const item = this.stack[this.stack.length - 1];
const minV = this.minV;
if (item < 0) {
return minV;
}
return item + minV;
};
/**
* @return {number}
*/
MinStack.prototype.min = function() {
return this.minV;
};
/**
* Your MinStack object will be instantiated and called as such:
* var obj = new MinStack()
* obj.push(x)
* obj.pop()
* var param_3 = obj.top()
* var param_4 = obj.min()
*/
Python Code:
class MinStack:
def __init__(self):
"""
initialize your data structure here.
"""
self.minV = float('inf')
self.stack = []
def push(self, x: int) -> None:
self.stack.append(x - self.minV)
if x < self.minV:
self.minV = x
def pop(self) -> None:
if not self.stack:
return
tmp = self.stack.pop()
if tmp < 0:
self.minV -= tmp
def top(self) -> int:
if not self.stack:
return
tmp = self.stack[-1]
if tmp < 0:
return self.minV
else:
return self.minV + tmp
def min(self) -> int:
return self.minV
# Your MinStack object will be instantiated and called as such:
# obj = MinStack()
# obj.push(x)
# obj.pop()
# param_3 = obj.top()
# param_4 = obj.min()
复杂度分析
- 时间复杂度:O(1)
- 空间复杂度:O(1)
两个栈
思路
我们使用两个栈:
- 一个栈存放全部的元素,push,pop都是正常操作这个正常栈。
- 另一个存放最小栈。 每次push,如果比最小栈的栈顶还小,我们就push进最小栈,否则不操作
- 每次pop的时候,我们都判断其是否和最小栈栈顶元素相同,如果相同,那么我们pop掉最小栈的栈顶元素即可
关键点
- 往minstack中 push的判断条件。 应该是stack为空或者x小于等于minstack栈顶元素
代码
JavaScript:
/**
* initialize your data structure here.
*/
var MinStack = function() {
this.stack = []
this.minStack = []
};
/**
* @param {number} x
* @return {void}
*/
MinStack.prototype.push = function(x) {
this.stack.push(x)
if (this.minStack.length == 0 || x <= this.minStack[this.minStack.length - 1]) {
this.minStack.push(x)
}
};
/**
* @return {void}
*/
MinStack.prototype.pop = function() {
const x = this.stack.pop()
if (x !== void 0 && x === this.minStack[this.minStack.length - 1]) {
this.minStack.pop()
}
};
/**
* @return {number}
*/
MinStack.prototype.top = function() {
return this.stack[this.stack.length - 1]
};
/**
* @return {number}
*/
MinStack.prototype.min = function() {
return this.minStack[this.minStack.length - 1]
};
/**
* Your MinStack object will be instantiated and called as such:
* var obj = new MinStack()
* obj.push(x)
* obj.pop()
* var param_3 = obj.top()
* var param_4 = obj.min()
*/
Python3:
class MinStack:
def __init__(self):
"""
initialize your data structure here.
"""
self.stack = []
self.minstack = []
def push(self, x: int) -> None:
self.stack.append(x)
if not self.minstack or x <= self.minstack[-1]:
self.minstack.append(x)
def pop(self) -> None:
tmp = self.stack.pop()
if tmp == self.minstack[-1]:
self.minstack.pop()
def top(self) -> int:
return self.stack[-1]
def min(self) -> int:
return self.minstack[-1]
# Your MinStack object will be instantiated and called as such:
# obj = MinStack()
# obj.push(x)
# obj.pop()
# param_3 = obj.top()
# param_4 = obj.min()
复杂度分析
- 时间复杂度:O(1)
- 空间复杂度:O(N)