4.6 KiB
4.6 KiB
Problem Link
https://leetcode.com/problems/subsets-ii/description/
Description
Given a collection of integers that might contain duplicates, nums, return all possible subsets (the power set).
Note: The solution set must not contain duplicate subsets.
Example:
Input: [1,2,2]
Output:
[
[2],
[1],
[1,2,2],
[2,2],
[1,2],
[]
]
Solution
Since this problem is seeking Subset not Extreme Value, dynamic programming is not an ideal solution. Other approaches should be taken into our consideration.
Actually, there is a general approach to solve problems similar to this one -- backtracking. Given a Code Template here, it demonstrates how backtracking works with varieties of problems. Apart from current one, many problems can be solved by such a general approach. For more details, please check the Related Problems section below.
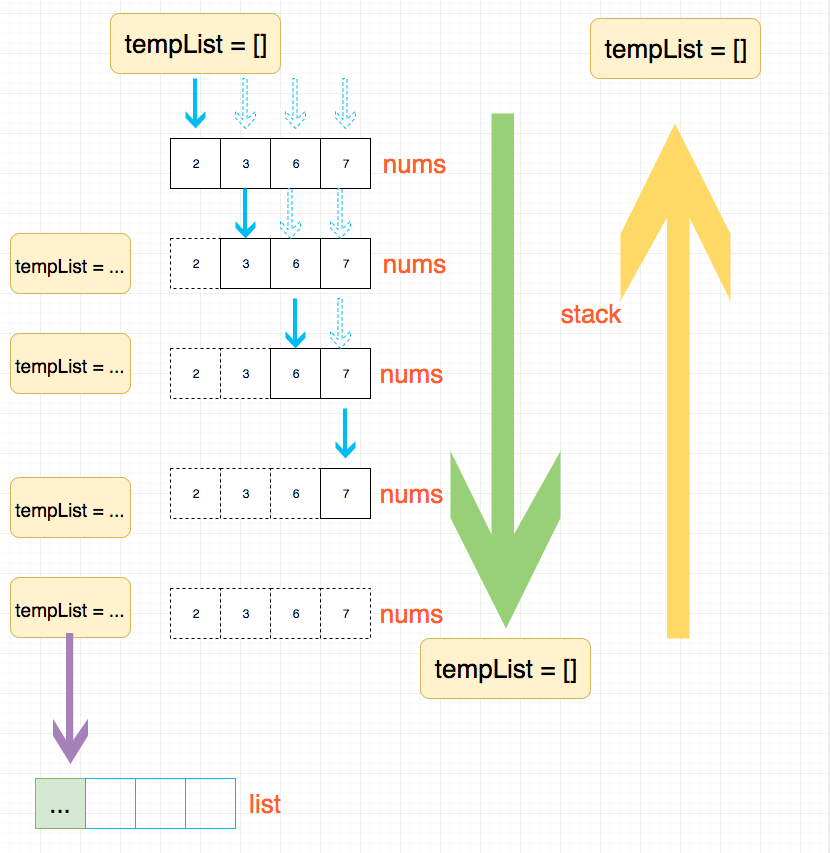
Given a picture as followed, let's start with problem-solving ideas of this general solution.
See Code Template details below.
Key Points
- Backtrack Approach
- Backtrack Code Template/ Formula
Code
- Supported Language:JS,C++,Python3
JavaScript Code:
/*
* @lc app=leetcode id=90 lang=javascript
*
* [90] Subsets II
*
* https://leetcode.com/problems/subsets-ii/description/
*
* algorithms
* Medium (41.53%)
* Total Accepted: 197.1K
* Total Submissions: 469.1K
* Testcase Example: '[1,2,2]'
*
* Given a collection of integers that might contain duplicates, nums, return
* all possible subsets (the power set).
*
* Note: The solution set must not contain duplicate subsets.
*
* Example:
*
*
* Input: [1,2,2]
* Output:
* [
* [2],
* [1],
* [1,2,2],
* [2,2],
* [1,2],
* []
* ]
*
*
*/
function backtrack(list, tempList, nums, start) {
list.push([...tempList]);
for(let i = start; i < nums.length; i++) {
//nums can be duplicated, which is different from Problem 78 - subsets
//So the situation should be taken into consideration
if (i > start && nums[i] === nums[i - 1]) continue;
tempList.push(nums[i]);
backtrack(list, tempList, nums, i + 1)
tempList.pop();
}
}
/**
* @param {number[]} nums
* @return {number[][]}
*/
var subsetsWithDup = function(nums) {
const list = [];
backtrack(list, [], nums.sort((a, b) => a - b), 0, [])
return list;
};
C++ Code:
class Solution {
private:
void subsetsWithDup(vector<int>& nums, size_t start, vector<int>& tmp, vector<vector<int>>& res) {
res.push_back(tmp);
for (auto i = start; i < nums.size(); ++i) {
if (i > start && nums[i] == nums[i - 1]) continue;
tmp.push_back(nums[i]);
subsetsWithDup(nums, i + 1, tmp, res);
tmp.pop_back();
}
}
public:
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
auto tmp = vector<int>();
auto res = vector<vector<int>>();
sort(nums.begin(), nums.end());
subsetsWithDup(nums, 0, tmp, res);
return res;
}
};
Python Code:
class Solution:
def subsetsWithDup(self, nums: List[int], sorted: bool=False) -> List[List[int]]:
"""Backtrack Approach: by sorting parameters first to avoid repeting sort later"""
if not nums:
return [[]]
elif len(nums) == 1:
return [[], nums]
else:
# Sorting first to filter duplicated numbers
# Note,this problem takes higher time complexity
# So, it could greatly improve time efficiency by adding one parameter to avoid repeting sort in following procedures
if not sorted:
nums.sort()
# Backtrack Approach
pre_lists = self.subsetsWithDup(nums[:-1], sorted=True)
all_lists = [i+[nums[-1]] for i in pre_lists] + pre_lists
# distinct elements
result = []
for i in all_lists:
if i not in result:
result.append(i)
return result
Related Problems
- 39.combination-sum(chinese)
- 40.combination-sum-ii(chinese)
- 46.permutations(chinese)
- 47.permutations-ii(chinese)
- 78.subsets
- 113.path-sum-ii(chinese)
- 131.palindrome-partitioning(chinese)