3.3 KiB
3.3 KiB
题目地址
https://leetcode.com/problems/3sum/description/
题目描述
Given an array nums of n integers, are there elements a, b, c in nums such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.
Note:
The solution set must not contain duplicate triplets.
Example:
Given array nums = [-1, 0, 1, 2, -1, -4],
A solution set is:
[
[-1, 0, 1],
[-1, -1, 2]
]
思路
我们采用分治的思想. 想要找出三个数相加等于0,我们可以数组依次遍历,
每一项a[i]我们都认为它是最终能够用组成0中的一个数字,那么我们的目标就是找到
剩下的元素(除a[i])两个相加等于-a[i].
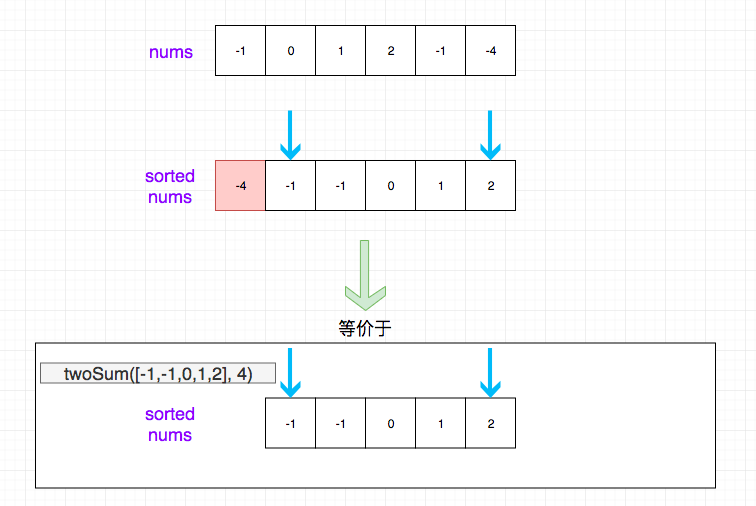
通过上面的思路,我们的问题转化为了给定一个数组,找出其中两个相加等于给定值,
这个问题是比较简单的, 我们只需要对数组进行排序,然后双指针解决即可。 加上我们需要外层遍历依次数组,因此总的时间复杂度应该是O(N^2)。
思路如图所示:
在这里之所以要排序解决是因为, 我们算法的瓶颈在这里不在于排序,而在于O(N^2),如果我们瓶颈是排序,就可以考虑别的方式了
如果找某一个特定元素,一个指针就够了。如果是找两个元素满足一定关系(比如求和等于特定值),需要双指针, 当然前提是数组有序。
关键点解析
- 排序之后,用双指针
- 分治
代码
/*
* @lc app=leetcode id=15 lang=javascript
*
* [15] 3Sum
*
* https://leetcode.com/problems/3sum/description/
*
* algorithms
* Medium (23.51%)
* Total Accepted: 531.5K
* Total Submissions: 2.2M
* Testcase Example: '[-1,0,1,2,-1,-4]'
*
* Given an array nums of n integers, are there elements a, b, c in nums such
* that a + b + c = 0? Find all unique triplets in the array which gives the
* sum of zero.
*
* Note:
*
* The solution set must not contain duplicate triplets.
*
* Example:
*
*
* Given array nums = [-1, 0, 1, 2, -1, -4],
*
* A solution set is:
* [
* [-1, 0, 1],
* [-1, -1, 2]
* ]
*
*
*/
/**
* @param {number[]} nums
* @return {number[][]}
*/
var threeSum = function(nums) {
if (nums.length < 3) return [];
const list = [];
nums.sort((a, b) => a - b);
for (let i = 0; i < nums.length; i++) {
//nums is sorted,so it's impossible to have a sum = 0
if (nums[i] > 0) break;
// skip duplicated result without set
if (i > 0 && nums[i] === nums[i - 1]) continue;
let left = i + 1;
let right = nums.length - 1;
// for each index i
// we want to find the triplet [i, left, right] which sum to 0
while (left < right) {
// since left < right, and left > i, no need to compare i === left and i === right.
if (nums[left] + nums[right] + nums[i] === 0) {
list.push([nums[left], nums[right], nums[i]]);
// skip duplicated result without set
while(nums[left] === nums[left + 1]) {
left++;
}
left++;
// skip duplicated result without set
while(nums[right] === nums[right - 1]) {
right--;
}
right--;
continue;
} else if (nums[left] + nums[right] + nums[i] > 0) {
right--;
} else {
left++;
}
}
}
return list;
};