3.6 KiB
3.6 KiB
题目地址(5. 最长回文子串)
https://leetcode-cn.com/problems/longest-palindromic-substring/
题目描述
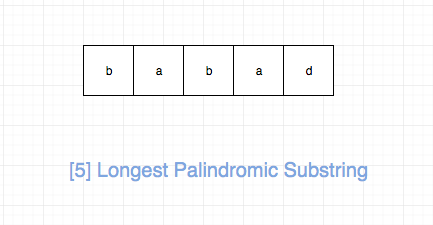
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1:
输入: "babad" 输出: "bab" 注意: "aba" 也是一个有效答案。 示例 2:
输入: "cbbd" 输出: "bb"
思路
这是一道最长回文的题目,要我们求出给定字符串的最大回文子串。
解决这类问题的核心思想就是两个字“延伸”,具体来说
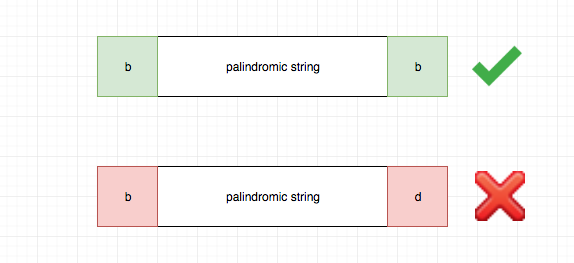
- 如果在一个不是回文字符串的字符串两端添加任何字符,或者在回文串左右分别加不同的字符,得到的一定不是回文串
- 如果一个字符串不是回文串,或者在回文串左右分别加不同的字符,得到的一定不是回文串
事实上,上面的分析已经建立了大问题和小问题之间的关联, 基于此,我们可以建立动态规划模型。
我们可以用 dp[i][j] 表示 s 中从 i 到 j(包括 i 和 j)是否可以形成回文, 状态转移方程只是将上面的描述转化为代码即可:
if (s[i] === s[j] && dp[i + 1][j - 1]) {
dp[i][j] = true;
}
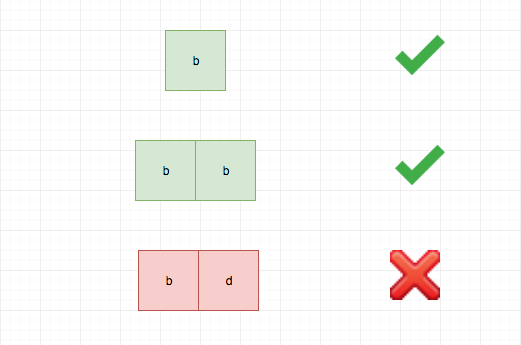
base case就是一个字符(轴对称点是本身),或者两个字符(轴对称点是介于两者之间的虚拟点)。
关键点
- ”延伸“(extend)
代码
代码支持:Python,JavaScript:
Python Code:
class Solution:
def longestPalindrome(self, s: str) -> str:
n = len(s)
if n == 0:
return ""
res = s[0]
def extend(i, j, s):
while(i >= 0 and j < len(s) and s[i] == s[j]):
i -= 1
j += 1
return s[i + 1:j]
for i in range(n - 1):
e1 = extend(i, i, s)
e2 = extend(i, i + 1, s)
if max(len(e1), len(e2)) > len(res):
res = e1 if len(e1) > len(e2) else e2
return res
JavaScript Code:
/*
* @lc app=leetcode id=5 lang=javascript
*
* [5] Longest Palindromic Substring
*/
/**
* @param {string} s
* @return {string}
*/
var longestPalindrome = function(s) {
// babad
// tag : dp
if (!s || s.length === 0) return "";
let res = s[0];
const dp = [];
// 倒着遍历简化操作, 这么做的原因是dp[i][..]依赖于dp[i + 1][..]
for (let i = s.length - 1; i >= 0; i--) {
dp[i] = [];
for (let j = i; j < s.length; j++) {
if (j - i === 0) dp[i][j] = true;
// specail case 1
else if (j - i === 1 && s[i] === s[j]) dp[i][j] = true;
// specail case 2
else if (s[i] === s[j] && dp[i + 1][j - 1]) {
// state transition
dp[i][j] = true;
}
if (dp[i][j] && j - i + 1 > res.length) {
// update res
res = s.slice(i, j + 1);
}
}
}
return res;
};
复杂度分析
- 时间复杂度:
O(N^2) - 空间复杂度:
O(N^2)
更多题解可以访问我的LeetCode题解仓库:https://github.com/azl397985856/leetcode 。 目前已经30K star啦。
大家也可以关注我的公众号《脑洞前端》获取更多更新鲜的LeetCode题解