11 KiB
Problem
https://leetcode.com/problems/maximum-subarray/
Problem Description
Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.
Example:
Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.
Follow up:
If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.
Solution
Below will explain 4 different approaches to solve this problem.
Solution #1 - Brute Force
Usually start from brute force when you don't have any idea, then step by step to optimize your solution.
Brute Force:(TLE)
Subarray sum, we then need to know subarray range [l, r], 2 for loop, list all possible subarrays, then 1 for loop to calculate current subarray sum,
using a global variable to keep track maxSum. This approach has very bad performance,time complexity is O(n^3).
Complexity Analysis
- Time Complexity:
O(n^3) - n array length - Space Complexity:
O(1)
Solution #2 - PrefixSum + Brute Force
Optimal brute force: (AC)
With brute force approach, we can precalculate prefixSum, so that no need to calculate subarray sum every time, time complexity can reduce to O(n^2)
calculate prefixSum, for giving subarray range [l,r],
current subarray sum: subarraySum = prefixSum[r] - prefixSum[l - 1];
global variable maxSum, compare every possible subarray sum to record max sum, maxSum = max(maxSum, subarraySum).
Complexity Analysis
- Time Complexity:
O(n^2) - n array length - Space Complexity:
O(n) - prefixSum array length n
If update original input array to represent prefix sum, then space will reduce to
O(1)
With this optimization, the time complexity is still too high, can we come up better optimization approach.
yes, optimized prefix sum
Solution #3 - optimized prefix sum - from @lucifer
we define S(i) ,use to calculate sum from range [0, i]。
then S(j) - S(i - 1) is sum of range [i, j].
Here, we can get all S[i] , (i = 0,1,2....,n-1) with one loop array.
at the same time, we get min sum from S[k], (k = 0,1,i-1), then
maxSum = max(maxSum, S[i] - minSum).
Here we maintain two variables minSum, maxSum.
Complexity Analysis
- Time Complexity:
O(n) - n array length - Space Complexity:
O(1)
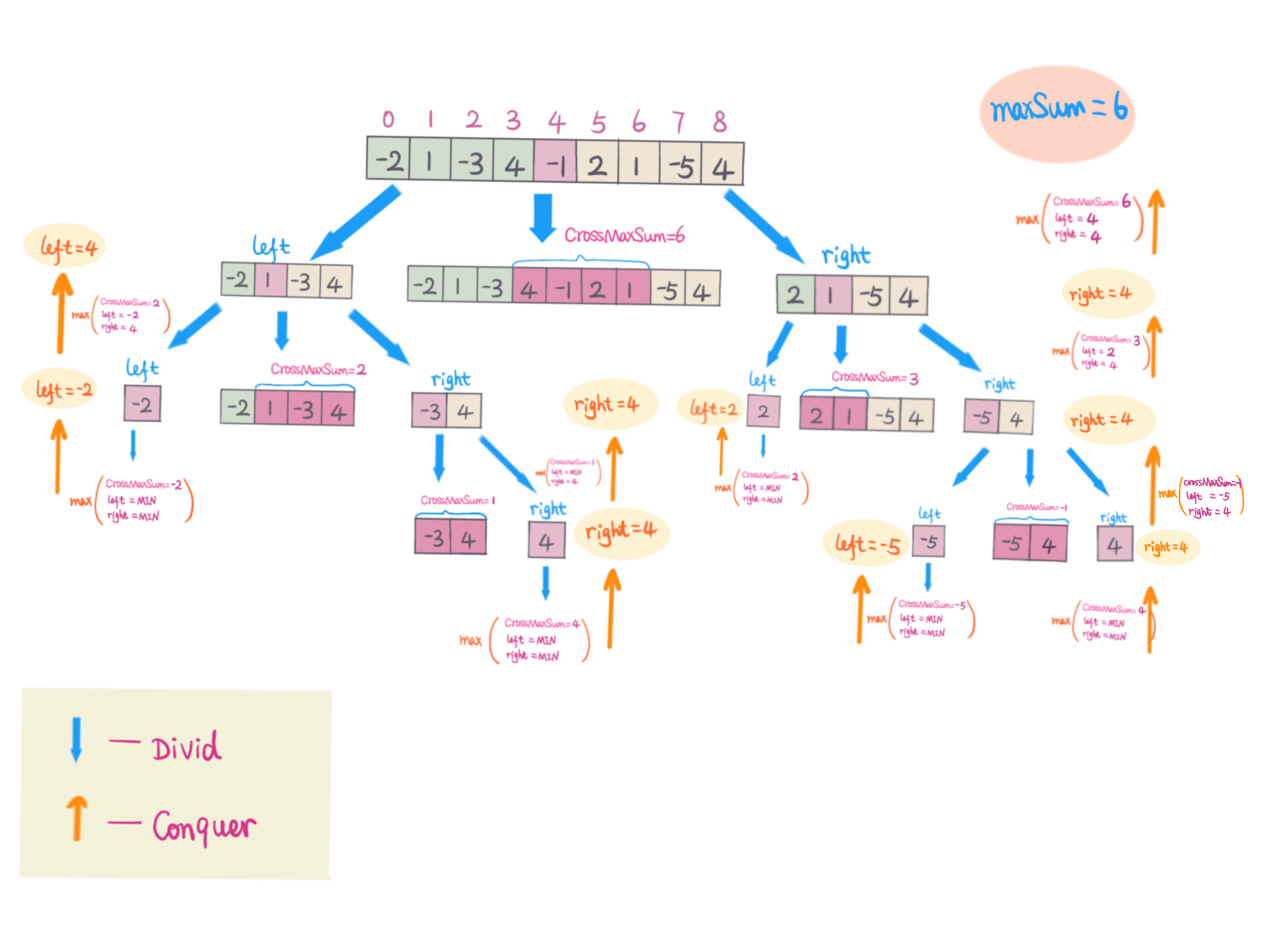
Solution #4 - Divide and Conquer
We partition array nums into two smaller arrays (left and right) from middle index m,
Then we have two arrays:
left = nums[0]...nums[m - 1]right = nums[m + 1]...nums[n-1]
The maximum subarray sum can be either one of below three maximum sum:
- Consider middle element
nums[m], Cross left and right subarray, the maximum sum is sum of
maximum left array suffix sum - leftMaxSum, maximum right array prefix sum - rightMaxSum and middle element - nums[m]
-> crossMaxSum = leftMaxSum + rightMaxSum + nums[m]
- Dont' contain middle element
nums[m], maxSum is inleft, left do recursive return max. - Don't contain middle element
nums[m], maxSum is inright, right do recursive return max.
The maximum sum is max(left, right, crossMaxSum)
For example, nums=[-2,1,-3,4,-1,2,1,-5,4]
Complexity Analysis
- Time Complexity:
O(nlogn) - n input array length - Space Complexity:
O(1)
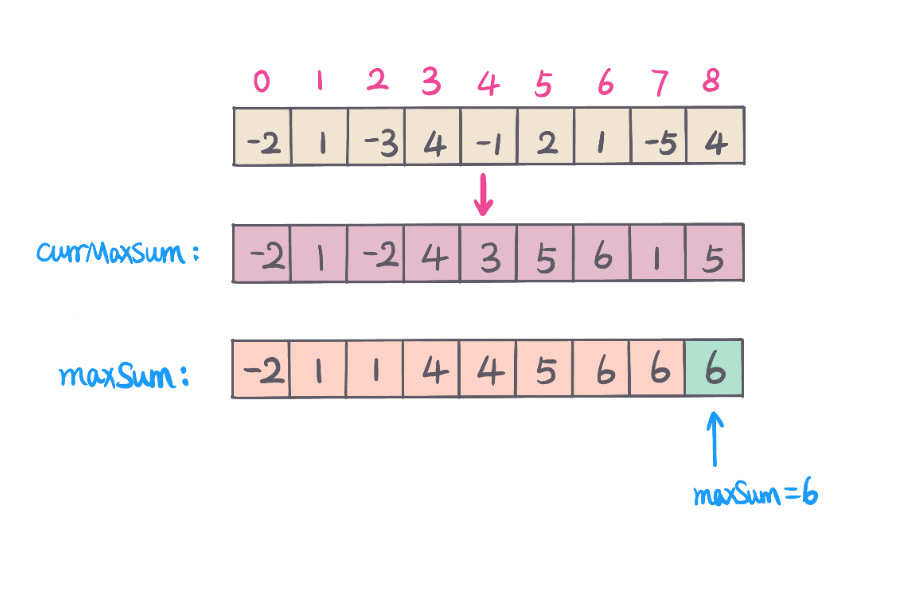
Solution #5 - Dynamic Programing
Key points of DP is to find DP formula and initial state. Assume we have
dp[i] - maximum sum of subarray that ends at index i
DP formula:
dp[i] = max(dp[i - 1] + nums[i], nums[i])
Initial state:dp[0] = nums[0]
From above DP formula, notice only need to access its previous element at each step. In this case, we can use two variables,
currMaxSum - maximum sum of subarray that must end with current index i.
maxSum - global maximum subarray sum
currMaxSum = max(currMaxSum + nums[i], nums[i]maxSum = max(currMaxSum, maxSum)
Complexity Analysis
- Time Complexity:
O(n) - n array length - Space Complexity:
O(1)
Key Points
- Brute force, list all possible subarray, calculate sum for each subarray (use prefixSum to optimize), return max.
- Divide and Conquer, from middle index, divide array into left and right part.
Recursively get left maximum sum and right maximum sum, and include middle element maximum sum.
return max(leftMaxSum, rightMaxSum, and crossMaxSum). - Dynamic Programming, find DP formula and initial state, and identify initial value, return maximum sum subarray。
Code (Java/Python3/Javascript)
Solution #2 - PrefixSum + Brute Force
Java code
class MaximumSubarrayPrefixSum {
public int maxSubArray(int[] nums) {
int len = nums.length;
int maxSum = Integer.MIN_VALUE;
int sum = 0;
for (int i = 0; i < len; i++) {
sum = 0;
for (int j = i; j < len; j++) {
sum += nums[j];
maxSum = Math.max(maxSum, sum);
}
}
return maxSum;
}
}
Python3 code (TLE)
import sys
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
n = len(nums)
maxSum = -sys.maxsize
sum = 0
for i in range(n):
sum = 0
for j in range(i, n):
sum += nums[j]
maxSum = max(maxSum, sum)
return maxSum
Javascript code from @lucifer
function LSS(list) {
const len = list.length;
let max = -Number.MAX_VALUE;
let sum = 0;
for (let i = 0; i < len; i++) {
sum = 0;
for (let j = i; j < len; j++) {
sum += list[j];
if (sum > max) {
max = sum;
}
}
}
return max;
}
Solution #3
Java code
class MaxSumSubarray {
public int maxSubArray3(int[] nums) {
int maxSum = nums[0];
int sum = 0;
int minSum = 0;
for (int num : nums) {
// prefix Sum
sum += num;
// update maxSum
maxSum = Math.max(maxSum, sum - minSum);
// update minSum
minSum = Math.min(minSum, sum);
}
return maxSum;
}
}
Python3 code
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
n = len(nums)
maxSum = nums[0]
minSum = sum = 0
for i in range(n):
sum += nums[i]
maxSum = max(maxSum, sum - minSum)
minSum = min(minSum, sum)
return maxSum
Javascript code from @lucifer
function LSS(list) {
const len = list.length;
let max = list[0];
let min = 0;
let sum = 0;
for (let i = 0; i < len; i++) {
sum += list[i];
if (sum - min > max) max = sum - min;
if (sum < min) {
min = sum;
}
}
return max;
}
Solution #4 - Divide and Conquer
Java code
class MaximumSubarrayDivideConquer {
public int maxSubArrayDividConquer(int[] nums) {
if (nums == null || nums.length == 0) return 0;
return helper(nums, 0, nums.length - 1);
}
private int helper(int[] nums, int l, int r) {
if (l > r) return Integer.MIN_VALUE;
int mid = (l + r) >>> 1;
int left = helper(nums, l, mid - 1);
int right = helper(nums, mid + 1, r);
int leftMaxSum = 0;
int sum = 0;
// left surfix maxSum start from index mid - 1 to l
for (int i = mid - 1; i >= l; i--) {
sum += nums[i];
leftMaxSum = Math.max(leftMaxSum, sum);
}
int rightMaxSum = 0;
sum = 0;
// right prefix maxSum start from index mid + 1 to r
for (int i = mid + 1; i <= r; i++) {
sum += nums[i];
rightMaxSum = Math.max(sum, rightMaxSum);
}
// max(left, right, crossSum)
return Math.max(leftMaxSum + rightMaxSum + nums[mid], Math.max(left, right));
}
}
Python3 code
import sys
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
return self.helper(nums, 0, len(nums) - 1)
def helper(self, nums, l, r):
if l > r:
return -sys.maxsize
mid = (l + r) // 2
left = self.helper(nums, l, mid - 1)
right = self.helper(nums, mid + 1, r)
left_suffix_max_sum = right_prefix_max_sum = 0
sum = 0
for i in reversed(range(l, mid)):
sum += nums[i]
left_suffix_max_sum = max(left_suffix_max_sum, sum)
sum = 0
for i in range(mid + 1, r + 1):
sum += nums[i]
right_prefix_max_sum = max(right_prefix_max_sum, sum)
cross_max_sum = left_suffix_max_sum + right_prefix_max_sum + nums[mid]
return max(cross_max_sum, left, right)
Javascript code from @lucifer
function helper(list, m, n) {
if (m === n) return list[m];
let sum = 0;
let lmax = -Number.MAX_VALUE;
let rmax = -Number.MAX_VALUE;
const mid = ((n - m) >> 1) + m;
const l = helper(list, m, mid);
const r = helper(list, mid + 1, n);
for (let i = mid; i >= m; i--) {
sum += list[i];
if (sum > lmax) lmax = sum;
}
sum = 0;
for (let i = mid + 1; i <= n; i++) {
sum += list[i];
if (sum > rmax) rmax = sum;
}
return Math.max(l, r, lmax + rmax);
}
function LSS(list) {
return helper(list, 0, list.length - 1);
}
Solution #5 - Dynamic Programming
Java code
class MaximumSubarrayDP {
public int maxSubArray(int[] nums) {
int currMaxSum = nums[0];
int maxSum = nums[0];
for (int i = 1; i < nums.length; i++) {
currMaxSum = Math.max(currMaxSum + nums[i], nums[i]);
maxSum = Math.max(maxSum, currMaxSum);
}
return maxSum;
}
}
Python3 code
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
n = len(nums)
max_sum_ending_curr_index = max_sum = nums[0]
for i in range(1, n):
max_sum_ending_curr_index = max(max_sum_ending_curr_index + nums[i], nums[i])
max_sum = max(max_sum_ending_curr_index, max_sum)
return max_sum
Javascript code from @lucifer
function LSS(list) {
const len = list.length;
let max = list[0];
for (let i = 1; i < len; i++) {
list[i] = Math.max(0, list[i - 1]) + list[i];
if (list[i] > max) max = list[i];
}
return max;
}
Follow Up
- When given M*N matrix, how to calculate maximum submatrix sum?
- When given array, return maximum product subarray? compare with maximum sum subarray, what is the difference?