2.2 KiB
场景
假设你现在要处理这样一个问题,你有一个网站并且拥有很多访客,每当有用户访问时,你想知道这个ip是不是第一次访问你的网站。
hashtable 可以么
一个显而易见的答案是将所有的ip用hashtable存起来,每次访问都去hashtable中取,然后判断即可。但是题目说了网站有很多访客,
假如有10亿个用户访问过,每个ip的长度是4 byte,那么你一共需要4 * 1000000000 = 4000000000Bytes = 4G , 如果是判断URL黑名单,
由于每个URL会更长,那么需要的空间可能会远远大于你的期望。
bit
另一个稍微难想到的解法是bit, 我们知道bit有0和1两种状态,那么用来表示存在,不存在再合适不过了。
加入有10亿个ip,我们就可以用10亿个bit来存储,那么你一共需要 1 * 1000000000 = (4000000000 / 8) Bytes = 128M, 变为原来的1/32, 如果是存储URL这种更长的字符串,效率会更高。
基于这种想法,我们只需要两个操作,set(ip) 和 has(ip)
这样做有两个非常致命的缺点:
- 当样本分布极度不均匀的时候,会造成很大空间上的浪费
我们可以通过散列函数来解决
- 当元素不是整型(比如URL)的时候,BitSet就不适用了
我们还是可以使用散列函数来解决, 甚至可以多hash几次
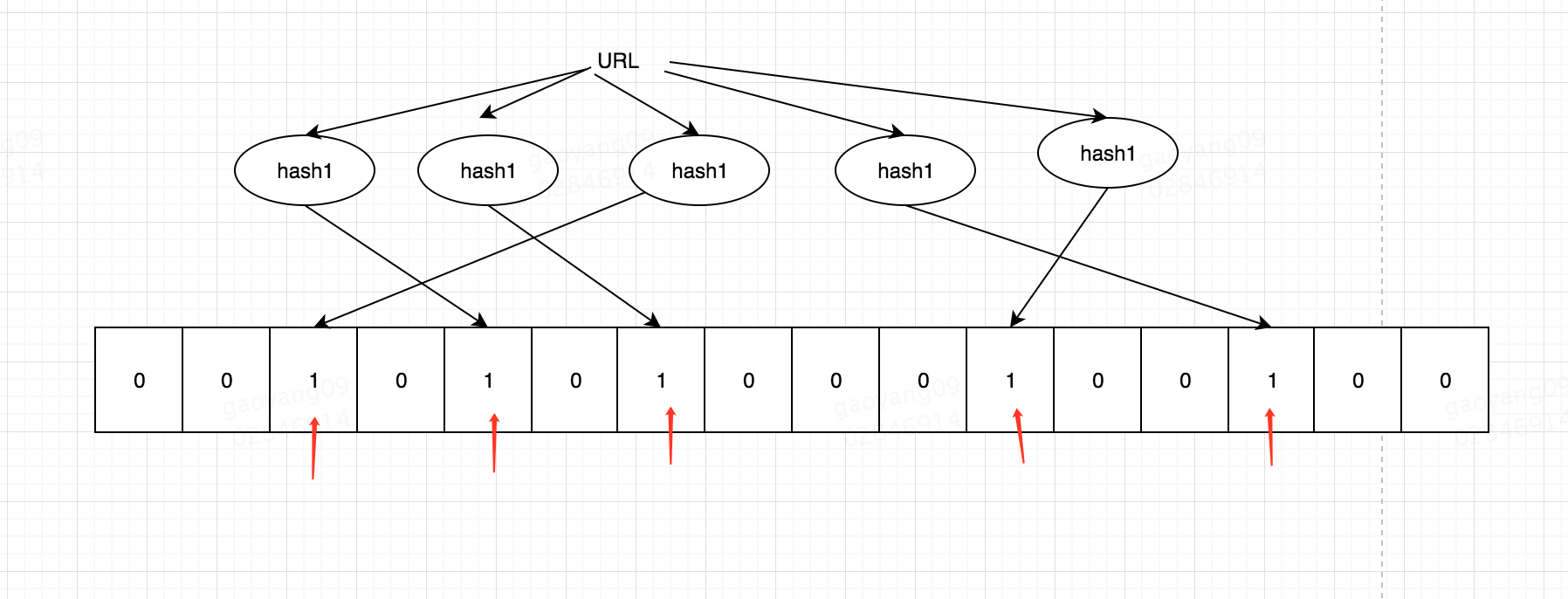
布隆过滤器
布隆过滤器其实就是bit + 多个散列函数, 如果经过多次散列的值再bit上都为1,那么可能存在(可能有冲突)。 如果
有一个不为1,那么一定不存在(一个值经过散列函数得到的值一定是唯一的),这也是布隆过滤器的一个重要特点。
布隆过滤器的应用
-
网络爬虫 判断某个URL是否已经被爬取过
-
K-V数据库 判断某个key是否存在
比如Hbase的每个Region中都包含一个BloomFilter,用于在查询时快速判断某个key在该region中是否存在。
- 钓鱼网站识别
浏览器有时候会警告用户,访问的网站很可能是钓鱼网站,用的就是这种技术
从这个算法大家可以对 tradeoff(取舍) 有更入的理解。